近日，物理与光电工程学院物理学系龙高平副教授在物理学学术期刊《Physics Letters B》（物理学 2区期刊）上发表文章《 Holonomy operator for spin connection in twisted geometry》（Phys. Lett. B 866 (2025) 139580）。该研究由龙高平副教授与西湖大学刘洪光老师共同合作完成。龙高平副教授为论文第一作者。

图 1. 文章发表页面截图

广义相对论和量子力学被视作现代物理学的两大支柱理论。基于这两个理论的许多研究结果（如广义相对论中的奇点问题）都暗示着需要将这两个理论有机地结合起来构造一个量子引力理论，并且在该方向的探索也是现代理论物理学中的一个关键且困难的研究课题。在构造量子引力的各种尝试性方案中，圈量子引力采用了非微扰的引力量子化方案且继承了广义相对论的核心思想——背景不依赖性，因此在世界范围内受到大量的研究者的重视。圈量子引力中的时空几何由所谓的twisted几何来描述。这种几何作为离散的Regge几何的推广，可以对圈量子引力的离散相空间作重参数化。然而，对于描述引力至关重要的自旋联络和曲率，在twisted几何中还没有一个清晰的刻画。

在本文的研究中，我们定义了圈量子引力中自旋联络的算符。具体来说，我们定义了twisted几何中的自旋联络的和乐，并且验证了该和乐的生成元在特定的连续性极限下给出了自旋联络（分布）场。进一步，通过使用和乐通量相空间的twisted几何参数化，并用通量算符替换通量，我们定义了twisted几何中自旋联络的和乐的算符。特别地，我们的方法通过引入依赖于loop的自旋联络的和乐，从而厘清了twisted几何中的自旋联络的不确定性，并且指出了这种不确定性与量子联络场是分布场有关（见图2）。因此，我们定义自旋联络的方法不仅适用于Regge几何，也可以自然地拓展到更广泛的twisted几何中的非Regge部分。

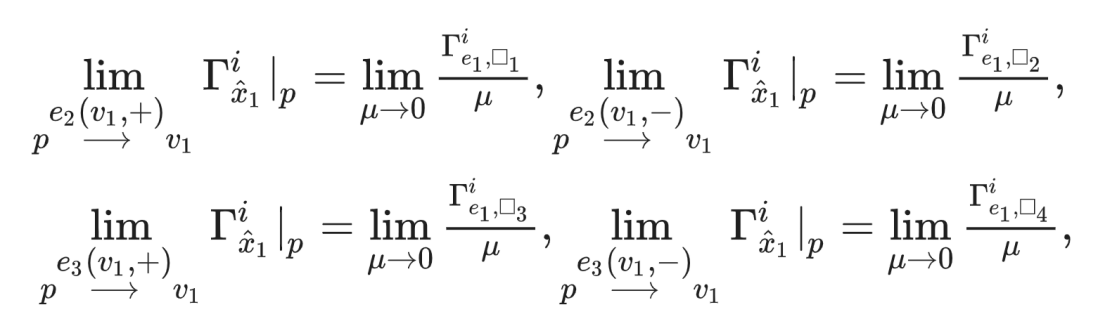
图 2.twisted几何中自旋联络的和乐依赖于loop，这种依赖与量子联络场是分布场有关

龙高平副教授近期致力于圈量子引力中量子几何与时空动力学的研究。 本次研究工作得到了国家自然科学基金项目的资助。

论文链接：

https://www.sciencedirect.com/science/article/pii/S0370269325003417?via%3Dihub

图文：龙高平

校对：陈科球

初审：黄晶晶

终审：幸江涛